- Home Page
- Kiddy Kites
- Cartoon Kite
A Cartoon Kite Collection
With a Different Twist
A cartoon kite is usually a diamond. Quite often, to the slight annoyance of many a kite fancier, the sticks are on the wrong side. Or the bridle is wrong or attached in an impossibly aft position—and so on!
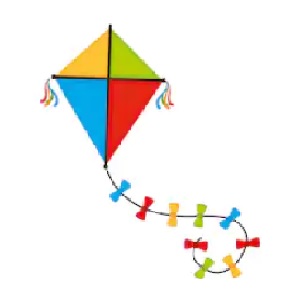 Typical illustration
Typical illustrationYep, I'm one of those fussy kite-fanciers. But perhaps it's better to just have a laugh at those mistakes rather than get annoyed.
Hence this page is a celebration of cartoon and clip-art kite stuff-ups.
Are you an experienced kite flier? Have a browse and a giggle. :-)
Just looking for clip art and arrived here by mistake? ;-) Hey, don't leave; you will learn plenty about single-line kites. And you'll have a laugh while you're at it!
I decided it would be most interesting to look at the "worst first." :-)
But down near the bottom, it finishes with a few examples of quite good depictions of kites. This proves that some cartoonists or line-art creators do actually know a thing or two about kites!
On this site, there's more kite-making info than you can poke a stick at. :-)
Want to know the most convenient way of using it all?
The Big MBK E-book Bundle is a collection of downloads—printable PDF files which provide step-by-step instructions for many kites large and small.
Every kite in every MBK series.
A Cartoon Kite Flown by the Tail!
No, I'm not kidding! Just take a look at these five:

And what's that bit coming from the nose? Weird.

Here's another confused cartoonist. And it's a very slack line with all those loops in it. Maybe a little jet engine is keeping the kite up there.
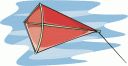
Is that line part of a tail? Shall we give the artist the benefit of the doubt? No, it really looks like it's meant to be a flying line, leading to a kite flier down below somewhere. Sigh.
And for a slight variation on the theme, some artists have chosen to attach the flying line to the same spot as the tail!
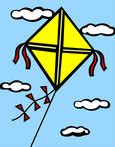
For a moment, I thought maybe the line was supposed to be going to a bridle on the far side of the sail. But no, it goes exactly to the tail end of the diamond!

In larger versions of this image, it's easier to see the little guy way below, holding the kite string. But look where it's attached.
Upside Down Diamond Kites!
You gotta be kidding me, I hear you say. Nope, here are three examples. I saw a few more than this too!
There are nice streamers on this attractive diamond-kite design—but it's the wrong way up!

This depicts sticks on the correct side, a realistic line angle, and a reasonable tail—but the diamond is inverted. Sheeesh.

There's a lot wrong with this image, but of course the up-side-down sail is the most obvious!
Interesting Bridles!
No wonder Joe Blow has difficulty getting the bridle right on his first attempt at making a kite. Check some of these out:
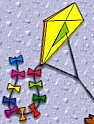
A downright strange cartoon kite, this is. :-) It has a keel like a delta, but another bridle line going right back to the tail end—not to mention the aft towing-point.

This one's a scream, isn't it! It must be caught in a mighty strong thermal is all I can say. Or perhaps it's a box windsock.

One leg of the bridle is attached to where the spars cross and the other goes to the bottom tip of the spar. The towing point is somewhere in between! It would never fly.

It's supposed to be a delta, and I think the nose is pointing to the left. One bridle leg goes to the nose while the others go somewhere near the wingtips. Interesting!

Now, if the horizontal spar was a little closer to the nose end of the kite and the spar was was stiff enough, this two-leg bridle would actually work! But it's certainly unconventional.
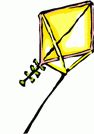
This next one is just as unconventional, with the addition of a bridle line going to the tail end. But, with no horizontal spar at all, this kite would just fold up and plummet to the ground!
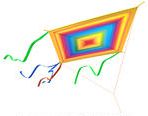
Sticks on the Wrong Side
To be fair, sometimes the sticks show through when the sail is lit from behind. That might have been the intention in some of these, but others are definitely wrong:
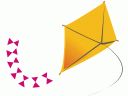
Apart from dihedral on the vertical spar, the sticks appear to be on the wrong side.

At first I thought they were the bridle, but it seems the two curved lines on this cartoon kite are supposed to represent the two spars. They're on the wrong side of the sail of course!
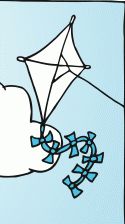
This is quite a reasonable-looking cartoon kite. To be kind, let's say the sail is clear plastic and the spars are just showing through... But somehow I doubt it!
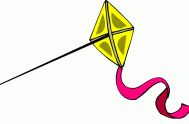
This cartoon kite is pretty blatant—unless that yellow sail is very translucent!

Now, there's no mistaking this artist's error! Tsk, tsk, tsk. The horizontal spar looks six times too heavy too.
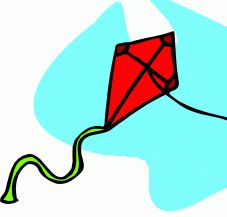
Here's another fairly reasonable-looking diamond in flight. But how see-through is that sail? I bet the artist tied the line directly to the sticks on the wrong side!
Aft Towing Points
In other words, these kites show the bridle towing point adjusted too far back toward the tail end. It's a bit more subtle, this one. But each cartoon kite below would not have a hope of flying as illustrated! However, most of these depictions do have the sticks on the correct side of the sail.

Here's a colored cow kite, being flown by a cow in the original cartoon! But the sail is square, with the line attached to where the sticks cross. So there's the same amount of sail area above and below the towing point. It would never fly.

There's a similar problem with this kite, not to mention the lack of a tail!
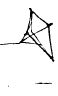
This has a weird three-leg bridle, no tail, and the towing point is way too low. Tsk, tsk, tsk. Tut, tut.
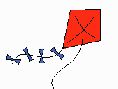
Mmmm this isn't bad at first glance, but the towing point is just too far aft.
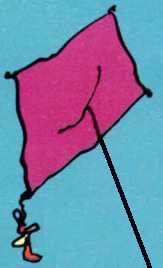
Although not extreme, it's the same for this one. The two-leg bridle appears to be under no tension!

And this one is similar, with a two-leg bridle.

The flying line is attached off to the side somewhere! And there's no tail.

Oooops! Try putting the tail on the other end of this kite, and it might fly.
A Very Heavy Cartoon Kite

This was from a German source, and I think the image was illustrating a point about making kites light in order to fly better. I think the rather ... umm chunky kite pictured would need a category 5 storm to have any hope of rising on its stri... I mean rope.
Many of the images on this page are cropped down considerably from the originals, to show just the kite in each case. Hence I hope to avoid stepping on anyone's toes from a copyright perspective! Other complete images are small less-detailed versions for the same reason.
Some Better Cartoon Kites
These images give a pretty respectable impression of a kite—sometimes in flight, sometimes not. Interestingly, the artists who know what a delta kite is, are usually able to get the keel and towing point right!

This black-and-white drawing has just a hint of a two-leg bridle. The artist has evidently flown a kite before, since it all looks "right." There are even pockets in the sail corners for the spar tips!

This butterfly kite is only an illustration, but it's credible.
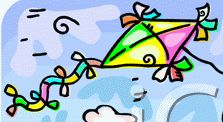
Again, this is only an illustration, but at least there are no obvious errors!

Maybe the towing point's a bit too low, but this is not a bad depiction of a diamond in flight.

How's this for a wonderful bird's-eye view of a colorful delta kite in flight—nice illustration.

Here's another similar view of a delta. This time it's towing a drogue for extra stability—and extra spectacle! The flying line curves up toward the central region, which is where deltas fly from. Tick.

Now, this one is not a freehand sketch. Having seen a larger version of the image, I think it was done using drawing software of some kind. It's a very precise depiction of a delta kite.
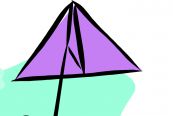
Here's a more impressionistic sketch of a delta kite, but it's basically correct.

This diamond kite is just hanging from its flying line. It looks "right." I give full marks to the cartoonist!
That's it. And if you recognize your work here, don't take offense! It's just a bit of fun for kite nuts. And maybe it might educate some people who are looking for cartoon-kite images.
As mentioned earlier, there's more kite making on this site than you can poke a stick at. :-)
Want to know the most convenient way of using it all?
The Big MBK E-book Bundle is a collection of downloads—printable PDF files that provide step-by-step instructions for many kites large and small.
That's every kite in every MBK series.
