- Home Page
- Kite Plans
- Area of a Kite
Area-of-a-Kite Calculation
A Practical Guide for Sticked Designs
Perhaps you have looked up how to find the area of a kite before. There's the familiar diamond shape, plus some info that looks or sounds like it came straight from a mathematics textbook.
 MBK Dowel Sode
MBK Dowel SodeAll this might be familiar enough for those with any sort of mathematical background, but that's not everyone is it! Not only that, but what if you wanted the area of a rokkaku, for example? Or even a dopero?
Down below, I start with a really handy method for finding the area of a kite—a simple delta or diamond. Aren't there plenty of those around!
Then there's an easy process for finding the area of a kite of more complex shape.
This is illustrated with the six-sided rokkaku and then a dopero. When you can follow these two shapes through, you should be able to calculate any area of a kite with straight sides and get the right answer! It's a step-by-step process and uses nothing more than simple arithmetic.
On this site, there's more kite-making info than you can poke a stick at. :-)
Want to know the most convenient way of using it all?
The Big MBK E-book Bundle is a collection of downloads—printable PDF files which provide step-by-step instructions for many kites large and small.
That's every kite in every MBK series.
Method For Two Simple Kite Shapes
If you just want to find the area of a simple delta or diamond, there is a very quick and easy way!
The distance from the vertical spar out to the "wingtip" multiplied by the kite's height (nose to tail) gives the total area of the kite. That's it!
Delta. For example, suppose your delta is 70 cm from nose to tail and 80 cm from vertical spar to wingtip, along the trailing edge. The whole sail has an area of 70 x 80 = 5,600 square centimeters or 5,600 / 10,000 = 0.56 square meters. That's just over half a square meter.
In inches, let's say your delta was 40 inches from nose to tail and 45 inches from vertical spar to wingtip. The whole sail has an area of 40 x 45 = 1,800 square inches or 1,800 / 144 = 12.5 square feet.
Diamond. Suppose you have bought yourself a diamond that is 110 cm tall and 100 cm across. The total area is the length from where the spars cross (out to the tip) multiplied by the height (nose to tail). So in this case, the total sail area is 110 x 50 = 5,500 square centimeters or 5,500 / 10,000 = 0.55 square meters.
In inches, let's say your diamond was 60 inches from nose to tail and 35 inches from vertical spar to wingtip. The whole sail has an area of 60 x 35 = 2,100 square inches or 2,100 / 144 = 14.6 square feet.
Note that some deltas actually have a diamond shape, with the trailing edge swept forward a little instead of going straight across. The calculation still works!
Now let's look at two more complex examples, using the following straightforward four-step process:
- Identify triangles, if any, in the half-sail template. Calculate the area of each one.
- Identify the remaining rectangles, if any. Calculate the area of each one.
- Add all those area figures together to get the template area.
- Multiply the template area by two to get the area of the whole kite. Done! Convert to other units if desired.
Both the "area of a kite" examples are worked in centimeters and inches, so you can follow in whatever system you are most comfortable with.
Area of a Kite
The Dowel Rokkaku

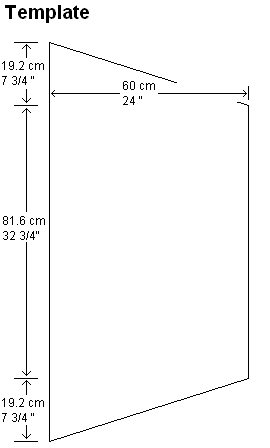

Step 1. From the diagram, you can see that the template shape contains two triangles. The area of each triangle is its width times its height, divided by two.
For triangle 1, in centimeters, that's 60 x 19.2 / 2 = 576 square centimeters.
In inches, that's 24 x 7 3/4 / 2 = 24 x 7.75 / 2 = 93 square inches. Note how measurements in inches need to be converted to decimal first. 1/4 = 0.25, 1/2 = 0.5 and 3/4 (as in this example) = 0.75
Triangle 2 is also 576 square centimeters or 93 square inches, since it has the same dimensions as triangle 1.
Step 2. From the diagram, you can see that the template shape contains 1 rectangle. The area of a rectangle is its width times its height.
So for rectangle 1, in centimeters, that's 60 x 81.6 = 4,896 square centimeters.
In inches, that's 24 x 32.75 = 786 square inches.
Step 3. Add all the areas. That's the two triangles and the rectangle, which is 576 + 576 + 4,896 = 6,048 square centimeters or 93 + 93 + 786 = 972 square inches.
Out in the Field
Rokkaku-kite stories of my real-life flying experiences are worth checking out!
Illustrated with photos and videos, of course.
Step 4. Double the template area and convert to other units if needed.
That's 6,048 x 2 = 12,096 square centimeters. Divide by 10,000 to get square meters if you want to: 12,096 / 10,000 = 1.21 square meters—well over 1 square meter.
Now for inches. 972 x 2 = 1,944 square inches. Divide by 144 to get square feet if you want to: 1,944 / 144 = 13.5 square feet.
Area of a Kite
The Dowel Dopero

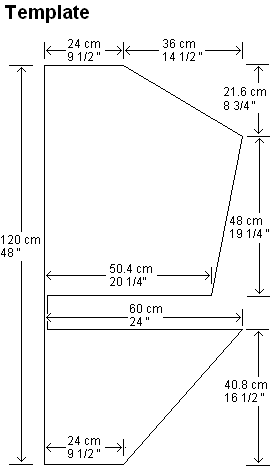
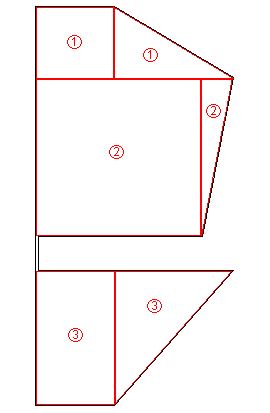
Step 1. From the diagram, you can see that the template shape contains three triangles. The area of each triangle is its width times its height, divided by two.
For triangle 1, in centimeters, that's 36 x 21.6 / 2 = 388.8 square centimeters.
In inches, that's 14 1/2 x 8 3/4 / 2 = 14.5 x 8.75 / 2 = 63.44 square inches. Note how measurements in inches need to be converted to decimal first. 1/2 = 0.5 and 3/4 = 0.75
The width of Triangle 2 is not marked on the template, so we have to figure it out from the measurements that are there. So the width is 60 - 50.4 = 9.6 cm. Hence the area is 9.6 x 48 / 2 = 230.4 square centimeters.
In inches, the width is 24 - 20 1/4 = 3 3/4 inches or 3.75 inches. Hence the area is 3.75 x 19.25 / 2 = 36.09 square inches.
The width of Triangle 3 is 60 - 24 = 36 cm. Hence the area is 36 x 40.8 / 2 = 734.4 square centimeters.
In inches, the width is 24 - 9 1/2 = 14 1/2 inches or 14.5 inches. The height is 16 1/2 inches or 16.5 inches. Hence the area is 14.5 x 16.5 / 2 = 119.63 square inches.
Step 2. From the diagram, you can see that the template shape contains three rectangles. The area of a rectangle is its width times its height.
So for rectangle 1, in centimeters, that's 24 x 21.6 = 518.4 square centimeters.
In inches, that's 9 1/2 x 8 3/4 = 9.5 x 8.75 = 83.13 square inches.
For rectangle 2, the area is 50.4 x 48 = 2,419.2 square centimeters.
In inches, that's 20 1/4 x 19 1/4 = 20.25 x 19.25 = 389.81 square inches.
For rectangle 3, the area is 24 x 40.8 = 979.2 square centimeters.
In inches, that's 9 1/2 x 16 1/2 = 9.5 x 16.5 = 156.75 square inches.
Step 3. Add all the areas. That's the three triangles and the three rectangles, which is 388.8 + 230.4 + 734.4 + 518.4 + 2,419.2 + 979.2 = 5,270.4 square centimeters or 63.44 + 36.09 + 119.63 + 83.13 + 389.81 + 156.75 = 848.85 square inches.
Out in the Field
Dopero-kite stories of my real-life flying experiences are worth checking out!
Illustrated with photos and videos, of course.
Step 4. Double the template area and convert to other units if needed.
That's 5,270.4 x 2 = 10,540.8 square centimeters. Divide by 10,000 to get square meters if you want to: 10,540.8 / 10,000 = 1.05 square meters—just over 1 square meter.
Now for inches. 848.85 x 2 = 1,697.7 square inches. Divide by 144 to get square feet if you want to: 1,697.7 / 144 = 11.79 square feet—nearly 12 square feet.
So this dopero has significantly less area than the rok and more spar material. But you wouldn't know it, from how well it flies in light wind!
Quicker Calcs With Rounding
So you don't need great accuracy for your sail-area figure? The dopero kite-shape example contains some awkward measurements. In the case of metric measurements, working with decimal places just means a few extra keystrokes on the calculator before the answer pops out. Still it can be useful to round the figures to make the "area of a kite" calculations quicker and easier.
For example, take a triangle that is 60.2 cm wide and 5.8 cm high. 60.2 is near enough to 60 and 5.8 is near enough to 6, so the area is 60 x 6 / 2 = 180 square centimeters. Compare that with the exact area of 174.58 square centimeters. 180 is close enough!
Rounding measurements is even more of a time saver when working with inches. Imagine a triangle with a width of 25 1/8 inches and a height of 4 3/4 inches. 25 1/8 is near enough to 25 and 4 3/4 is near enough to 5, so the area is 25 x 5 / 2 = 62.5 square inches. Compare that with the exact area of 59.67, which is not very far off!
Furthermore, when adding several area figures together, the errors tend to cancel each other out. The resulting overall area of a kite figure is often much more accurate than you might expect!
Flat Versus Projected Area of a Kite
In the real world, kites don't fly with perfectly flat sails, of course. The effective, or projected, sail area of a kite is somewhat smaller, affected by:
- Dihedral or bow of the horizontal spar(s)
- Billow in the sail due to air pressure in flight
The easiest way to visualize projected area of a kite is to imagine holding it with nose and tail the same short distance off the ground. Gravity causes some billow in the sail, similar to when the kite is flying. This is on a sunny day, with the sun directly overhead. (I won't go into all the circumstances that need to come together for this to be the case!) Now, look at the shadow of the sail on the ground. This is the projected area of the sail.
My guess is that for most flat or bowed kites, the projected area is somewhere between 2 and 20 percent less than the flat area. So if you are calculating the area of a kite for the purpose of selecting line strength, you could factor this in, to be even more accurate.
Finally...
If you've had a bit of fun finding the area of a kite by running these calculations, you could try one of my barn door or sode designs just as an exercise. Apart from that small nose section, there are no triangles at all in the MBK Dowel Sode!
I hope you have found this discussion about finding the area of a kite useful. May your flying line never snap!
As mentioned earlier, there's more kite making on this site than you can poke a stick at. :-)
Want to know the most convenient way of using it all?
The Big MBK E-book Bundle is a collection of downloads—printable PDF files which provide step-by-step instructions for many kites large and small.
That's every kite in every MBK series.
